INTRODUCCIÓN Y ANTECEDENTES

El presente artículo, elaborado a partir de investigaciones llevadas a cabo para los postgrados Máster de Economía Agraria, Alimentaria y de los Recursos Naturales de la Universidad Politécnica de Madrid (UPM) y Máster en Investigación en Economía de la Universidad Nacional de Educación a Distancia (UNED), consiste en la elaboración de un modelo estadístico de predicción para el consumo en hogar de vino de calidad en España. Para ello es necesario un estudio en profundidad de las series de datos de consumo de dicha bebida en los hogares españoles, utilizándose para ello herramientas estadísticas y econométricas. Una vez analizadas estas series temporales se procederá a la elaboración del modelo y a la realización de las comprobaciones pertinentes.

El Ministerio de Agricultura, Pesca y Alimentación de España ha apostado fuertemente en los últimos tiempos por la investigación de los mercados, recopilando toda la información posible para tratar de dar las mejores respuestas posibles a una sociedad cuyos hábitos alimenticios no dejan de cambiar. Del mismo modo, las empresas privadas demandan de manera creciente una información ordenada, estudiada y debidamente actualizada para no perder competitividad. El hecho de que instituciones públicas y privadas puedan contar con predicciones confiables de consumos y precios hace que este campo tenga un especial y creciente interés. El punto de partida de este proyecto es el Panel Alimentario del Ministerio, donde se recogen datos de consumo y precio de todos los grupos de alimentos, mes a mes, desde el año 1987. Esto supone una muestra de gran calidad analítica al ser estable, continua y bien definida, elaborada a partir de recogida de datos de más de 6000 hogares y con el respaldo de la Administración Pública. Obviamente, el hecho de poder hacer un estudio cuantitativo de 30 años de consumo y precios permite sacar conclusiones relevantes y, sobre todo, realizar modelos y predicciones muy potentes, cada vez más demandadas, pero aún no demasiado estudiadas ni explotadas.

En los estudios previos a este trabajo se contó con la inestimable tutela del profesor Jesús Javier Litago de la Escuela Técnica Superior de Ingeniería Agronómica, Alimentaria y de Biosistemas de Madrid, quien lleva décadas estudiando esta parcela del conocimiento por su interés en la alimentación y la agricultura y de cuyos trabajos salen las principales referencias para llevar a cabo este proyecto. No sólo sus estudios publicados como Judez y Litago (1993) o Litago y Terraza (1994) han sido de gran interés, también los trabajos guiados por él como García-Badell (2005) o Dávila (2017). En el apartado de Referencias se encuentra el resto de estos trabajos. Y, por supuesto, también se cuenta con los importantes estudios −como el de análisis de series temporales y construcción de modelos ARIMA− de Box, Jenkins, Reinsel y Ljung (2016), el de análisis de correlación cruzada de Sims (1972) y los de análisis espectral de Granger (1969) y de Reinsel (1981). Finalmente, otros trabajos actuales fueron revisados por su interés metodológico y econométrico para la realización de estos estudios, algunos de ellos son: Pérez Rodrigo et al. (2020), Limache Sandoval (2021) y Ramírez Castañeda et al. (2021).

METODOLOGÍA

Box y Jenkins (1976) desarrollaron una metodología destinada a identificar, estimar, y diagnosticar modelos de series temporales para variables cuantitativas en cualquier ámbito científico-técnico con el objetivo de predecir y orientar su control. Esta metodología se basa en la utilización de los datos de la variable para identificar las características de su estructura probabilística subyacente, en contraposición a los procedimientos tradicionales de identificación de modelos basados en una teoría explicativa del fenómeno en estudio. En este proyecto se utilizan fundamentalmente los modelos ARIMA propuestos por Box y Jenkins para el análisis de una variable (univariantes) en función de su pasado y de una serie de variables aleatorias.

RESULTADOS Y DISCUSIÓN

Identificación de las características dinámicas de las series de tiempo

La serie de vino de calidad (desde ahora CAL) presenta un problema: el Ministerio de Agricultura, Pesca y Alimentación no pudo proporcionar los datos de consumo desde enero de 2013 a febrero de 2015 (ambos inclusive), pero se consideran los datos relativamente irrelevantes para entender el comportamiento de la serie ya que los datos anteriores y posteriores continúan una tendencia y permiten suponer lo que ocurrió con los datos que faltan. En cualquier caso, alguna de las gráficas (como la Fig. 1) presenta anomalías por este hecho.

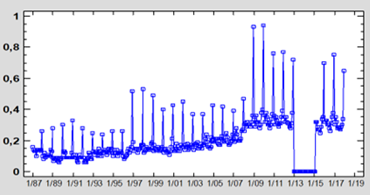
Figura 1. Evolución del consumo mensual de CAL en los hogares españoles en el período 1978-2017.

Una vez dicho esto, el consumo mensual de vino de calidad (CAL) ha experimentado una ligera tendencia ascendente a lo largo de la serie, más intensa en el período 2007-2009 como se aprecia en la en los consumos acumulados anuales. A partir de este último año presenta una tendencia negativa que perduró hasta 2017. Al mismo tiempo se observa en la serie una regular y muy marcada estacionalidad a lo largo de todo el período que queda de manifiesto en el consumo medio mensual. Dicha evolución anual se resume en un muy marcado máximo en diciembre, con motivo de las festividades navideñas, y un consumo más o menos constante a lo largo de los demás meses del año. La media de esta serie presenta un valor de 0,2, una mediana de 0,16 y una desviación típica de 0,14. Todo ello sugiere que la serie es no estacionaria y estacional.

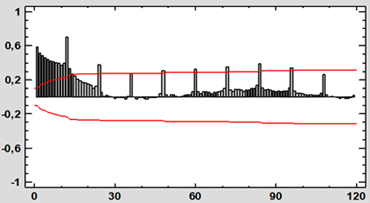
Figura 2. Función de Autocorrelación de CAL 1987-2017

La función de autocorrelación de CAL (Fig. 2) muestra varias dinámicas. En primer lugar, los coeficientes disminuyen lentamente hasta el entorno del retardo 40 y luego comienzan de nuevo a incrementarse durante varios retardos. Por otro lado, son muy significativos los retardos estacionales (12, 24, 36…). En cuanto al Peridograma de CAL (Fig. 3) presenta su máxima ordenada en el último período (372) lo que demuestra la tendencia a largo plazo de la serie, y también presenta varios picos diferenciados que corresponden al período 12 y a los armónicos de 12 (6, 4, 3, 2.4 y 2) y que certifican la estacionalidad de la serie.

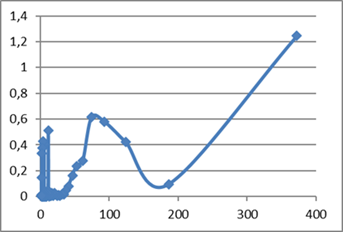
Figura 3. Peridograma de la serie CAL

Las estimaciones del estadístico τ del test de Dickey-Fuller (DF) para la serie son inferiores en valor absoluto a los valores críticos para 1% y 5% para los dos modelos empleados. Por tanto, se confirma la presencia de raíz unitaria (tendencia) en CAL y la necesidad de tomar sus primeras diferencias para construir correctamente un modelo de predicción para dicha serie. En la Figura 4 se muestra la gráfica de D_CAL (Diferencias de CAL) comparándola con la de la serie original. En el punto siguiente se ahonda en los detalles y características de esta nueva serie que presenta una evolución estacionaria en media con ciclos no regulares en valor, pero sí en frecuencia.

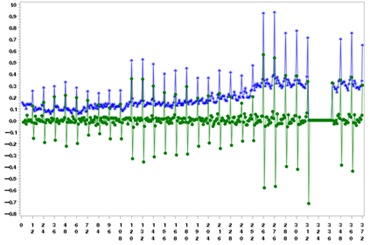
Figura 4. Primeras diferencias de MES (D_MES) y serie original

Estudio de la serie de primeras diferencias

Después de ver y estudiar la gráfica de D_CAL en el punto anterior se pasa al estudio de la función de autocorrelación y del Peridograma de esta nueva función para asegurar que es adecuado para construir el modelo. La función de autocorrelación de la Figura 5 muestra unos coeficientes significativos en los retardos estacionales (12, 24…) y también unos coeficientes relevantes justamente anteriores y posteriores a los estacionales (1, 11, 13, 23…). Por su parte el Peridograma (del que se hablará también en el punto siguiente) presenta su ordenada máxima en el período 3 y ordenadas significativas en 12 y en el resto de sus armónicos, lo que denota su estacionalidad.

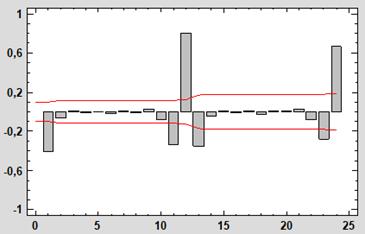
Figura 5. Función de Autocorrelación de la serie D_CAL

Mayoritariamente la ordenada máxima se da en el período 12, algo muy característico de la presencia de estacionalidad, pero en el caso del vino de calidad (DCAL) la máxima ordenada se encuentra en el período 3, armónico de 12, lo que implica también estacionalidad. En este caso en el orden 12, a pesar de que sus ordenadas principales se encuentran en sus armónicos, se presenta una ordenada reducida y no significativa, lo que no afecta a la estacionalidad.

Los valores del test de Fisher-Kappa (FK) que se han obtenido son muy superiores a los valores críticos del test para 200 ordenadas al 1 y 5%, 9,71 y 8,15 por lo que se rechaza la hipótesis de que la serie es ruido blanco y no puede rechazarse la significación de la componente estacional representada por la ordenada máxima. El test de Bartlett-Kolmogorov-Smirnov (BKS) presenta en este caso un P-value muy cercano a cero, confirmando por ello la significación de la estacionalidad (Fuller, 1976).

Estimación y validación del modelo

El modelo seleccionado para la serie CAL es un SARIMA (0,1,2)x(0,0,3), que incluye la transformación de primeras diferencias junto a los parámetros constante, media móvil regular (MA) y (SMA) media móvil estacional (orden 12) que se pueden encontrar en la Tabla 1. Todos los parámetros estimados, excepto la constante, presentan estadísticos t de Student superiores a 2 (en valor absoluto) por lo que el modelo es correcto.

Tabla 1

Estimación de un modelo SARIMA para la variable CAL

Parámetro	Estimación	Error Stnd.	t	P-valor
MA(1)	0.48588	0.0524105	9.27065	0.000000
MA(2)	0.117035	0.0521895	2.24251	0.025528
SMA(1)	-0.798384	0.0527303	-15.1409	0.000000
SMA(2)	-0.380258	0.0674058	-5.64132	0.000000
SMA(3)	-0.23528	0.0621424	-3.78614	0.000179
Mean	0.000175365	0.00344917	0.0508426	0.959479
Constante	0.000175365

Los residuos del modelo seleccionado muestran una evolución estacionaria y aleatoria. La función de autocorrelación (Figura 6) no muestra ningún coeficiente significativo en los primeros 25 retardos y el Peridograma (Figura 7) presenta ordenadas muy poco significativas, lo que indica que estos residuos son ruido blanco.

Figura 6. Función de autocorrelación de los residuos del modelo estimado para CAL

La hipótesis nula de ausencia de autocorrelación en los residuos del modelo estimado para CAL no se rechaza por el test Ljung-Box (1978), ya que su estadístico Q toma un valor de 26.51, que es inferior al valor de una χ2 para un nivel de significación del 5% y 24 grados de libertad (36.42). Por lo que no se puede rechazar que dichos residuos son completamente aleatorios y no contienen información, por lo que el modelo resulta válido para predecir CAL.

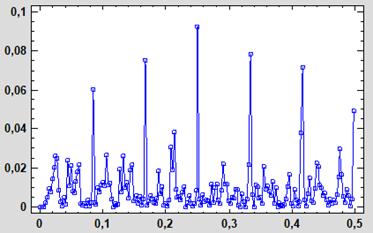
Figura 7. Peridograma de los residuos del modelo estimado para CAL

Predicción y evaluación

En este punto se presentan las predicciones obtenidas con el modelo propuesto para el consumo del vino de calidad. Primeramente, se hacen predicciones ‘ex post’, es decir predicciones de la propia serie de datos del año 1987 al 2017, se compara con los datos reales y se obtienen los errores de predicción de estas. Posteriormente, se llevan a cabo las predicciones ‘ex ante’, hacia delante, una predicción de los 12 meses siguientes al último de la serie (diciembre 2017), es decir, predice el consumo para los 12 meses de 2018. Esta predicción se compara con los datos mes a mes del último año y se acota su rango de error como se puede apreciar en la gráfica a continuación (Figura 8).

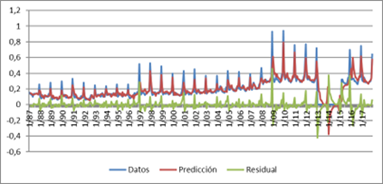
Figura 8. Gráfico de la predicción ‘ex post’ para CAL

En general, las predicciones ‘ex post’ de los consumos presentan una alta coincidencia con los datos en el período 1987-2017. Solamente encontramos un tramo en el cual el modelo no actúa correctamente, era de suponer ya que coincide con el tramo de meses para los cuales el Ministerio no pudo proporcionar datos, el resto de las predicciones son correctas, tanto anteriores como posteriores a este tramo anómalo. El error de predicción es, de la misma manera, aceptablemente bajo, estable y aleatorio en todos los casos para el horizonte de predicción.

Figura 9. Gráfico de la predicción ‘ex ante’ para CAL

Por su parte, las predicciones ‘ex ante’ (Figura 9) del consumo presentan una coincidencia muy alta con los datos observados los doce meses siguientes al final de la muestra, situándose por encima y por debajo de ellos a lo largo de todo el horizonte de predicción y coincidiendo repetidas veces de forma exacta. El error de predicción es muy bajo y el modelo puede ser aceptado para predecir la variable.

CONCLUSIONES

Este trabajo aporta una sólida visión histórica de la evolución del consumo del vino de calidad (CAL) en los hogares españoles y un análisis econométrico exhaustivo de su serie temporal desde 1987 a 2018, lo que arroja una idea muy clara de las tendencias previas a la pandemia de COVID-19. Por otro lado, se ha podido mostrar en profundidad y aplicar la metodología Box y Jenkins (1976) de modelos ARIMA para series de datos que permite proponer modelos y testarlos correctamente para poder validarlos y comenzar a obtener las primeras predicciones.

En definitiva, se ha conseguido satisfactoriamente el fin último del trabajo que no era otro que llegar a un modelo de predicción válido para poder prever la evolución futura de la variable estudiada: la del consumo en España de vino de calidad en los hogares.

Las tendencias registradas y el modelo propuesto pueden entroncarse en consonancia con trabajos relacionados como Frenquel Mattiazzi et al. (2019), Martín-Grande (2018) o Lasanta et al. (2023) para construir una visión más completa de este subsector de gran relevancia en el mercado agroalimentario nacional español y, también, en el mercado internacional.

Este trabajo es la continuación de otros anteriores, con la ventaja y el valor añadido de contar con una serie temporal más amplia (lo que permite conseguir modelos cada vez más robustos y eficaces), y, al mismo tiempo, es un punto de inicio para posibles nuevos estudios de mayor amplitud que aborden el problema desde más puntos de vista y permitan entender mejor el pasado de las series y predecir de una manera cada vez más precisa lo que sucederá en el futuro. Así mismo, este artículo podría ser el comienzo de otro estudio más ambicioso que englobara todos los grupos y subgrupos alimentarios y que llevara más allá la elaboración de modelos de predicción y relación.

CONTRIBUCIÓN DE LOS AUTORES

El autor llevó a cabo la totalidad del trabajo: concepción y diseño del estudio, recopilación y análisis de los datos, interpretación de resultados y redacción del manuscrito.

AGRADECIMIENTOS

Este trabajo no hubiese sido posible sin las enseñanzas de Jesús Javier Litago, profesor de la Escuela de Ingenieros Agrónomos de Madrid. Asimismo, esta investigación es resultado del aprendizaje de dos programas de postgrado: el Máster de Economía Agraria de la Universidad Politécnica de Madrid y el Máster en Investigación en Economía de la Universidad Nacional de Educación a Distancia. Por último, el autor quiere expresar su agradecimiento a la Universidad Rey Juan Carlos, al Programa Interuniversitario DEcIDE y a la Universidad Nacional de Educación a Distancia por su apoyo institucional y al Banco Santander por la ayuda financiera en algunas de las fases de elaboración de este artículo.

REFERENCIAS BIBLIOGRÁFICAS

Box, G. E. P.; Jenkins, G. M. (1976). Time Series Analysis, Forecasting and Control. Ed. Holden-Day. https://doi.org/10.1111/jtsa.12194

Buffiere, C. (1995). L’analyse de co-intégration entre les séries de prix des marchés de gros des asperges de Madrid et Perpignan. Memoire de Maitrise. Université de Montpellier.

Buys Ballot, C. (1847). Les Changements périodiques de tempèrature. Kemink et Fils.

Dávila, S. (2017). Definición de un modelo predictivo para analizar la evolución de los precios de la carne de cerdo y su relación con parámetros de calidad en la materia prima, alimentación y tendencias de mercado. Esc. Técnica Superior de Ingeniería Agronómica, Alimentaria y de Biosistemas.

Dickey, D. & Fuller, W. (1979). Distribution on the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association, 74 (366), 427-431.

https://doi.org/10.1080/01621459.1979.10482531

Dickey, D. & Fuller, W. (1981). Likelihood ratio statistic for autoregressive time series with a unit root. Econometrica, 49, 1057-1072.

https://doi.org/10.2307/1912517

Escofier, B. & Pagès, J. (1988). Analyses Factorielles Simples et Multiples: Objetifs, Methodes et Interprétation. Dunot Editions.

Frenquel Mattiazzi, I.; Pérez Hernández, S. & Sancho Cabrera, V. M. (2019). Análisis del consumo de vino y cerveza en España. Universidad de La Laguna.

Fuller, W. A. (1976). Introduction to Statistical Time Series. Ed. John Wiley & Sons.

García Badell, L. (2005). Evolución de los Hábitos Alimentarios en los Hogares Españoles: Análisis Multivariante y de Series Temporales del Panel de Consumo del MAPA (1987-2003). Escuela Técnica Superior de Ingenieros Agrónomos.

Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37, 424-438.

https://doi.org/10.2307/1912791

Johnston, J. (1980). Métodos de econometría. Vicens-Vives Universidad.

Judez, L. (1989). Técnicas de Análisis de Datos Multidimensional. Bases teóricas y aplicaciones a la Agricultura. Ministerio de Agricultura, Pesca y Alimentación. Secretaría General Técnica.

Judez, L.; Litago, J. J. & Terraza, M. (1993). Análisis de las series de precios al consumo del espárrago en España mediante modelos dinámicos univariantes. Investigación Agraria, 8(3).

Litago, J. J. & Terraza, M. (1994). Analyse de la Stationnarite et de la Saisonnalite de la Consommation Familiale des Vins Espagnols. Une étude de la substitution entre boissons. Université de Montpellier.

Litago, J. J. & Terraza, M. (1997). Relations dynamiques de court terme entre les consommations de boissons des ménages espagnols. Cahier Scientifique, 1.

Litago, J. J. & Terraza, M. (1998). Analyse dynamique de la consommation des boissons en Espagne”. Cahier Scientifique, 2.

Llorca, V. (1994). Étude économetrique du marché des vins de Jerez. Maîtrise Économetric, Université de Montpellier.

Ljung, G. & Box, G. (1978). On a measure of lack of fit in time series models. Biometrika, 65(2), 297-303. https://doi.org/10.1093/biomet/65.2.297

Martín-Grande, P. A. (2018). Econometric models and of prediction of the alimentary consumption in the Spanish homes. Group of Earth Observation for Quantitative Biosphere Dynamics (UPM).

Martínez, T. L.; Romero, M. E. N. & López, R. S. (2023). Vineyards and wine between 1995 and 2019. Cuadernos de investigación geográfica, 49(1), 211-230. https://doi.org/10.18172/cig.5646

Matilla García, M.; Pérez Pacual, P. & Sanz Carnero, B. (2017). Econometría y Predicción. McGraw-Hill/Interamericana y UNED.

Peña, D. (2005). Análisis de series temporales. Alianza Editorial.

Pulido, A. & López, A. (1999). Predicción y simulación aplicada a la economía y gestión de empresas. Ediciones Pirámide.

Ramírez, L. N.; Cruz, S. L. C. & Leguízamo, J. A. C. (2021). Modelos de fluctuaciones de precios agrícolas: Estudio comparativo de frutas tropicales frescas en Colombia. Revista de ciencias sociales, 27(4), 197-212.

Rodrigo, C. P.; Citores, M. G.; Bárbara, G. H.; Litago, F. R.; Saenz, L. C.; Bartrina, J. A.; ... & Majem, L. S. (2020). Cambios en los hábitos alimentarios durante el periodo de confinamiento por la pandemia COVID-19 en España. Spanish journal of community nutrition, 26(2), 6.

Sandoval, E. M. L. (2021). Modelo ARIMA sobre el consumo de agua de uso poblacional en la ciudad de Tacna. Veritas Et Scientia, 10(1), 69-82. https://doi.org/10.47796/ves.v10i1.461

Sanjuán, A.; Gil, J. M. & Albisu, L. M. (1994). Una aproximación a la medición de la incidencia de los precios agrarios en los precios al consumo de los alimentos (1987-1992). Monografías INIA, 94.

Sevilla, C. (1997). Analyse econometrique du complexe francais des boissons. Memoire de Maitrise. Université de Montpellier.

Uriel Jiménez, E. (1985). Análisis de Series Temporales. Modelos ARIMA. Paraninfo.